Language Modeling Is Compression 论文阅读
1. 概述
这是DeepMind 最近发表的一篇论文,题目翻译成中文是“语言模型即压缩”,是一个很简单但也有分量的观点。更有趣的是,论文中作者发现,自己的预训练大模型Chinchilla 70B只在文本训练集上训练后,在ImagNet 图像Patch上压缩率能达到43.4%,优于PNG算法的压缩率58.5%,在LibrSpeech语音数据集上,压缩率达到16.4%,优于语音压缩算法FLAC30.3%的压缩率。
说实话看到这个结论我还是很震惊的。一个是文本数据上训练的模型居然也能用于图像和语音的压缩,而且压缩率还高于常用的领域特定的压缩算法。
除了震惊,还很好奇大模型是怎么被当作压缩器来压缩文本图像和语音数据的。在好奇心的驱使下,我读了几遍这篇论文。
除了上面的结论外,论文中作者提供了许多有启迪的观点,比如:
- 通过推导,说明了压缩最优即是预测最优,即压缩和预测的等价性
- 传统压缩算法的特点是上下文很长(比如gzip 32K字节),可以利用具有丰富信息的上下文来进行压缩算法的设计,而Transformer结构的语言模型则是上下文很短(比如2048字节),通过大量参数来调节压缩的结果
- Transformer模型是基于tokenizer压缩的数据进行训练的,因此tokenizer也是一种压缩器
- 从最右压缩算法的角度来看,语言模型作为压缩器,最优的模型大小是和数据强绑定的,不可能无限扩大,从这个角度一定程度给出了LLM的理论上限
- 传统压缩算法也能当作一种生成模型,给语言模型的研究带来新的可能性
在这篇论文阅读文章中,我尝试就这些结论和几个关心的问题给出自己的解读,如有不准确之处,欢迎指出。
2. 为什么说压缩即预测
作者首先是介绍了信息论的一些基本理论,然后结合语言模型的优化目标,引出了压缩最优即是预测最优。具体过程下面展开。
对一个序列(如“AIXI”),无损压缩的过程是将其转换为一种高效的表示(如01序列),同时能从该表示序列中恢复出原始的数据。无损压缩其实是一种编码过程。
对于一个离散随机变量,其信息熵表示为H(X),计算公式为H(X) = - ∑ P(x) log2 P(x),其中,P(x)表示随机变量X取值为x的概率。
根据香农的信息熵理论,对于最优的编码方案,平均编码长度L至少应该不小于信息熵H(X)。当编码长度等于信息熵时,即L = H(X),编码达到了最优。
算术编码 (Arithmetic Coding) 是一种高效的无损压缩算法,是一种最优编码。概括来说,它将每个编码区间按照待编码序列的概率分布来进行划分,对于出现概率更大的序列元素,赋予更大的编码区间。下图演示了算数编码的过程,可以看到将4字节的输入编码为了7bit的输出,压缩率为7/(4x8) = 21.8%。具体算术编码的算法细节可以参考这篇文章。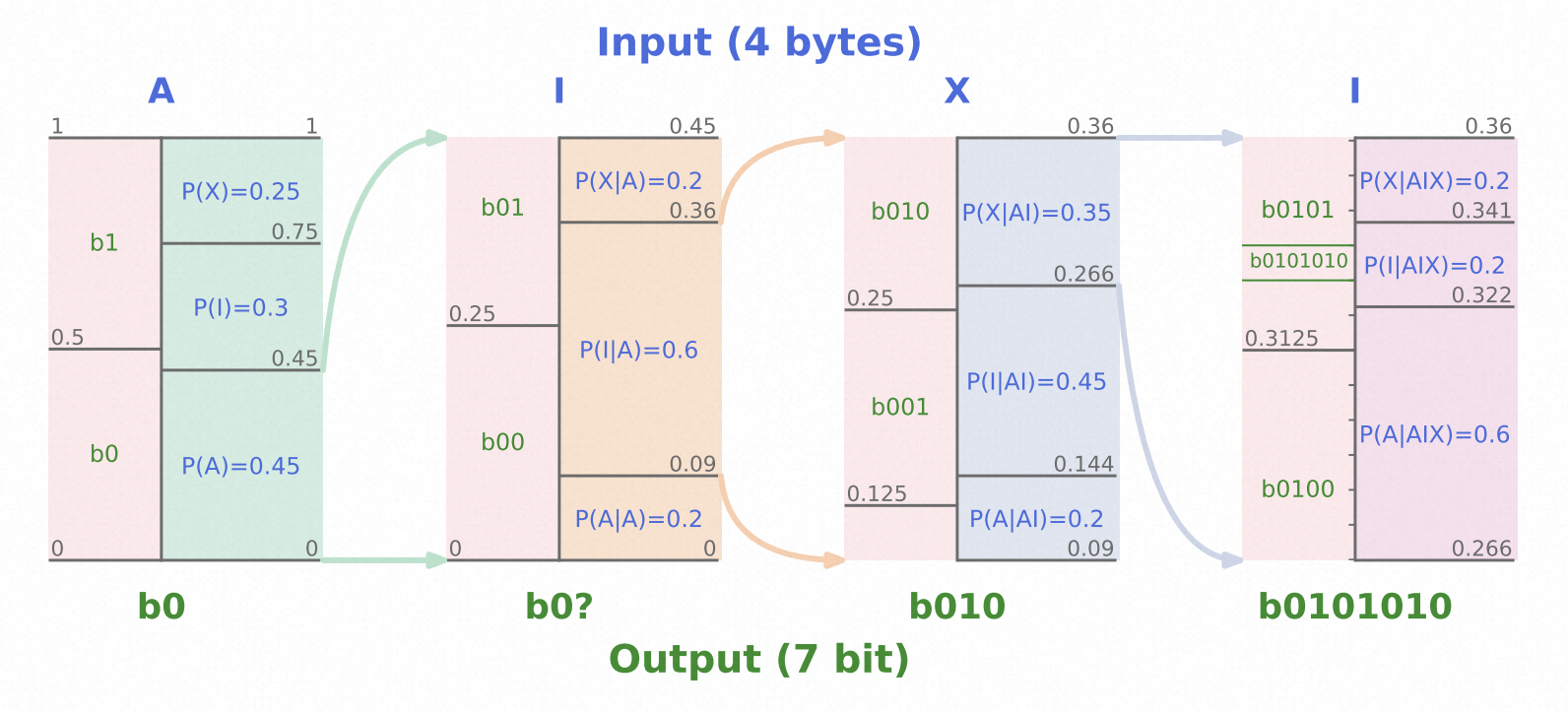
实际情况中,表示随机变量X取值为x的概率P(x)经常是难以获得的,因此采用P^来近似。基于这种近似,最优编码的期望长度如下,实际是一种交叉熵的表示。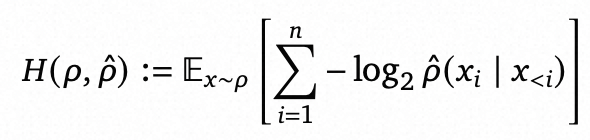
这个表达式也刚好是现有语言模型的loss优化目标,也就是说,最小化压缩率等价于最小化语言模型的loss,即最优压缩即最优语言模型,从而证明了压缩和预测的等价性。
总结来说,这一部分根据压缩的最优目标和语言模型Loss的一致性,推导出两者其实是等价的。
3. 语言模型如何进行压缩
3.1 压缩算法选择
对于传统压缩算法,作者选择了两个通用的压缩算法和两个特定模态的压缩算法。通用的压缩算法选择的是gzip和LZMA2。gzip相信大家都不陌生,用过linux的人都应该见过。而LZMA2是7z使用的压缩算法。这两者都算是久经考验的使用广泛的生产环境压缩算法,虽然不见得是最前沿的。
图像领域的压缩算法是PNG,语音领域的压缩算法是FLAC,两者都是无损压缩算法。
作为对比的语言模型选择了两个系列的大小不同的模型,比较小的是vanilla的只有decoder的 Transformer结构,在enwiki8上预训练(注意没有在别的数据上finetune)。比较大的是DeepMind之前提出的Chinchilla 系列模型,也只在文本上训练,没有见过图像和语音数据。
3.2 数据设置
数据集的选择也是很有技巧。首先是对于传统压缩算法和LLM,应用场景大相径庭,该怎么选择测试集进行合理的比较呢。
对于语言模型,由于常见模型输入context是2048,因此选择了把数据切分成N段2048字节的数据,来进行测试。
对于传统压缩算法,显然是可以将整个数据都作为整体进行压缩的,而切分成小块进行压缩是对结果有损害的。所以作者对传统压缩算法采用了两种处理方式。
为了方便比较不同模态的数据,作者都是构造总大小为1GB的数据集。
文本数据,作者采用了截止到2006年3月3日的维基百科英文预料的前1e8个字节,作为enwiki8,前1e9字节作为enwiki9。可以看到,enwiki8是包含在enwiki9中的,而enwiki9刚好是1G Bytes。
图像数据采用的是ImageNet数据集,选择了488821张图片,每张图片选择32x64的patch,然后转换为灰度图(每个像素刚好1个字节),刚好是488821x32x64=1G Bytes。
语音数据是从LibriSpeech数据集中选择的,每段2048字节,选择了488821段,也是刚好1G字节。
3.3 如何进行数据压缩
对于语言模型进行数据压缩的细节,论文没有描述,我只能说一下我的猜测。作者采用算术编码的方式,根据给定每个输入后模型的输出的概率,利用概率大小划分编码空间,对序列中所有输入元素执行完一次推理,得到最终的编码结果。
3.4 压缩结果
下面的表格展示了整体的压缩结果。
chunk size 无穷大表示不进行数据的切分,也就是传统压缩算法的压缩过程。
压缩率等于压缩后文件大小/原始文件大小,其中Raw压缩率没有考虑模型尺寸大小,二调整后的压缩率将模型的参数量也计算进了压缩后的文件大小中,由于语言模型参数量很大,因此调整后的压缩率甚至超过了一百。
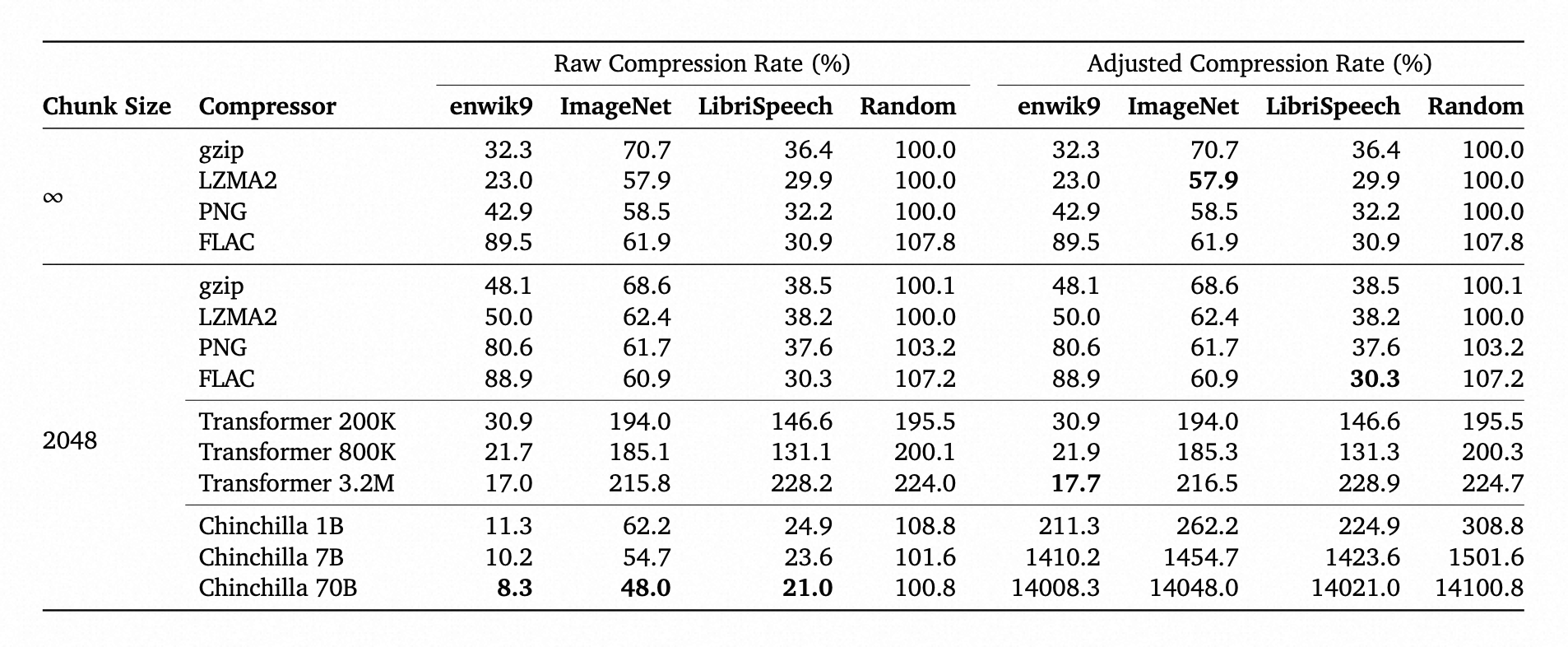
从这个表格中可以得出一些结论:
- 传统压缩算法经过分块,确实有比较大的性能下降,说明大的上下文信息对压缩至关重要
- 针对图像设计的压缩算法PNG在语音数据上LibrSpeech也能得到较好的压缩结果
- LZMA2通用压缩算法在LibriSpeech数据上压缩率优于语音特定的FLAC算法,还是有点出乎意料
- 由于传统压缩算法没有模型参数,因此调整后压缩率等于Raw压缩率
- 在enwik8上训练的Transformer模型,增大参数后在同模态的enwiki9上效果会变好,而在不同模态的图片和语音数据上,增大参数量到一定程度后效果反而下降
- 而Chinchilla语言模型参数量从1B到7B再到70B,压缩性能都是在稳步提升,与Vanilla Transformer呈现不同的现象
下面图中是在enwiki8上预训练到不同参数量的Transformer在enwiki7/8/9上的压缩率,其中压缩率是调整后压缩率,也就是考虑了参数量。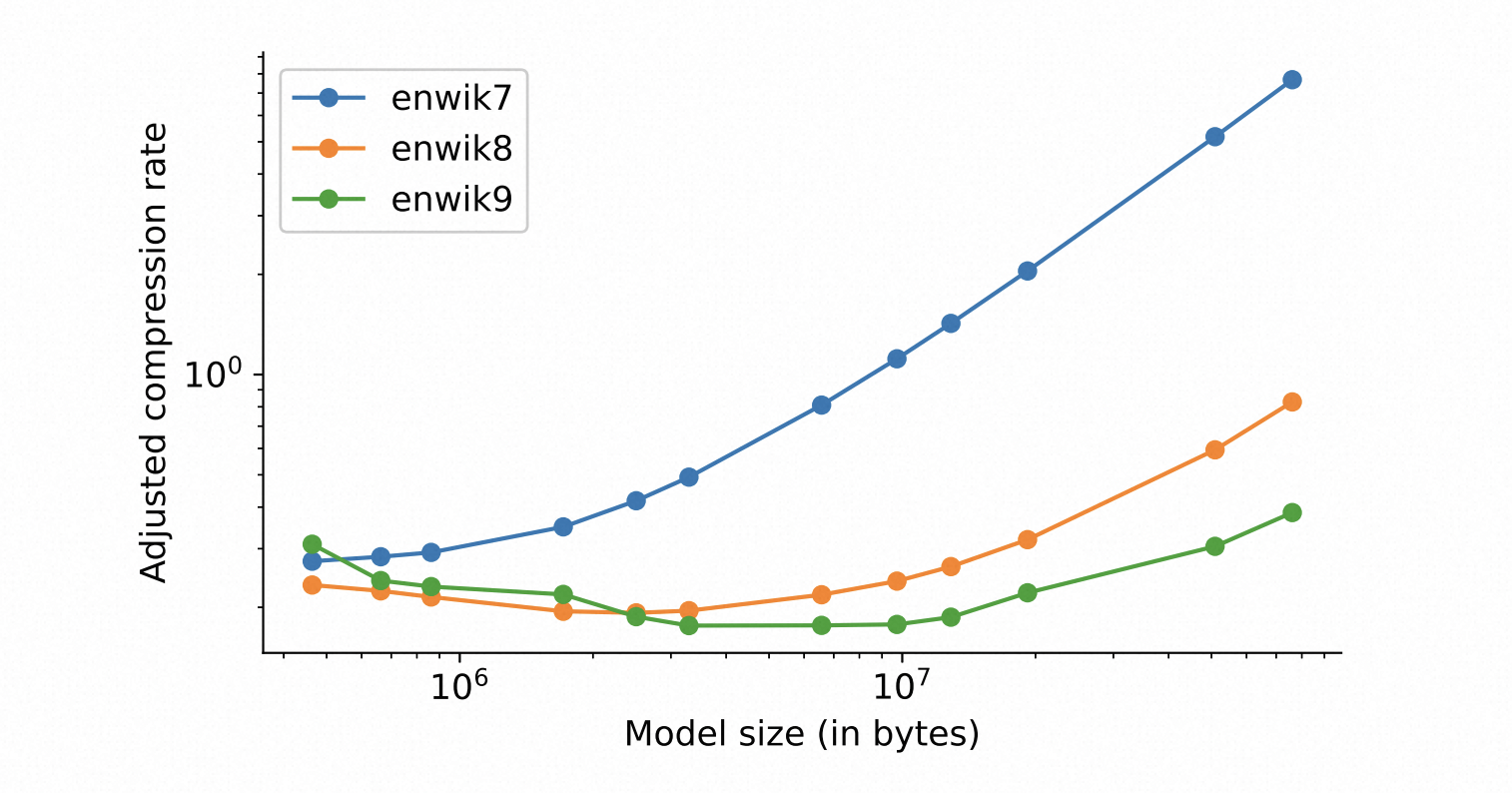
从这里可以看出一些结论:
- 随着参数量的增大,压缩性能都下降了(表现为压缩率增大),这是因为参数量的增大对结果的影响比较大
- 对于大的数据集(enwiki9),更多参数的模型压缩性能更好,但更大的模型在小的数据集上效果比较差,也就是说从压缩的角度看,模型的Scaling,与测试集的大小有关
为了对比不同压缩算法的生成能力,作者比较了gzip和Chinchilla 70B 在文本,图像和语音上的生成能力,具体来说,给出前面的的内容(文本是前1948个字节预测最后100个字节,图像和语音是给出前面一半预测后面一半),让算法来预测后面一半的内容。注意这个生成过程和压缩过程是不同的。
文本预测结果如下
可以看到语言模型预测的结果更连贯,而gzip预测的结果则没有明显的含义
语音预测上,gzip的预测更自然一些,而语言模型的预测则进入了循环,类似大家使用代码补全模型时经常会遇到的循环一样,不知道是不是同样的效应。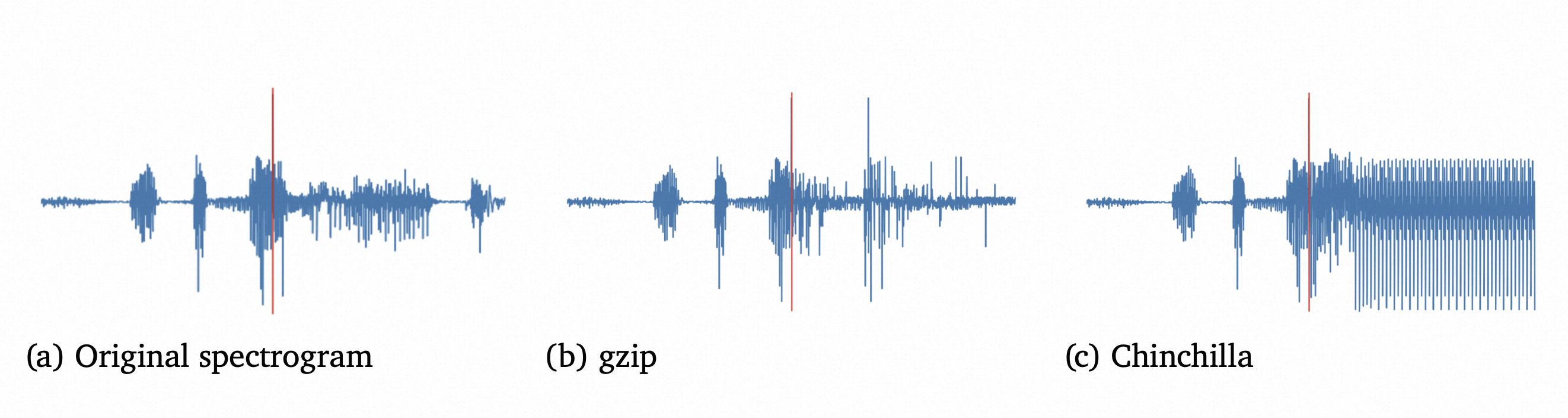
图像生成方面,语言模型和gzip都是从已知的图像信息中预测颜色值,不过两者的分布还是挺不一样的,gzip像是水平和竖直方向规律的噪声,而语言模型则明显的更能体验row-wise的效应。
另外一个实验是关于序列长度对压缩性能的影响。可以看到增大序列长度,三个任务上所有压缩算法的压缩性能都提升了。而Chinchilla 的压缩性能最好。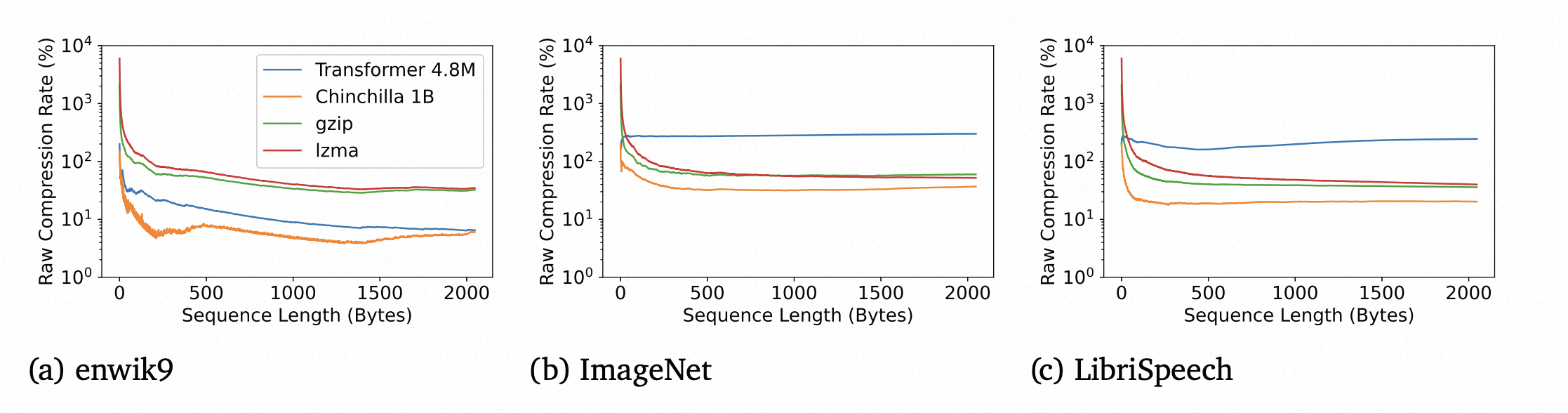
理论上来讲,gzip,lzma等传统压缩算法在序列长度增大后继续增大压缩性能,直到达到非切块场景的效果。
然后作者还比较了在Vanilla Transformer结构上,采用不同tokenization方法在3个不同参数的网络上的Raw压缩率。可以看到,对于比较小的网络(200K),增大tokenization的词汇大小能提高压缩性能,但针对大模型,增大词汇量压缩性能变差,可以看到tokenization的选择对结果还是有挺大影响的。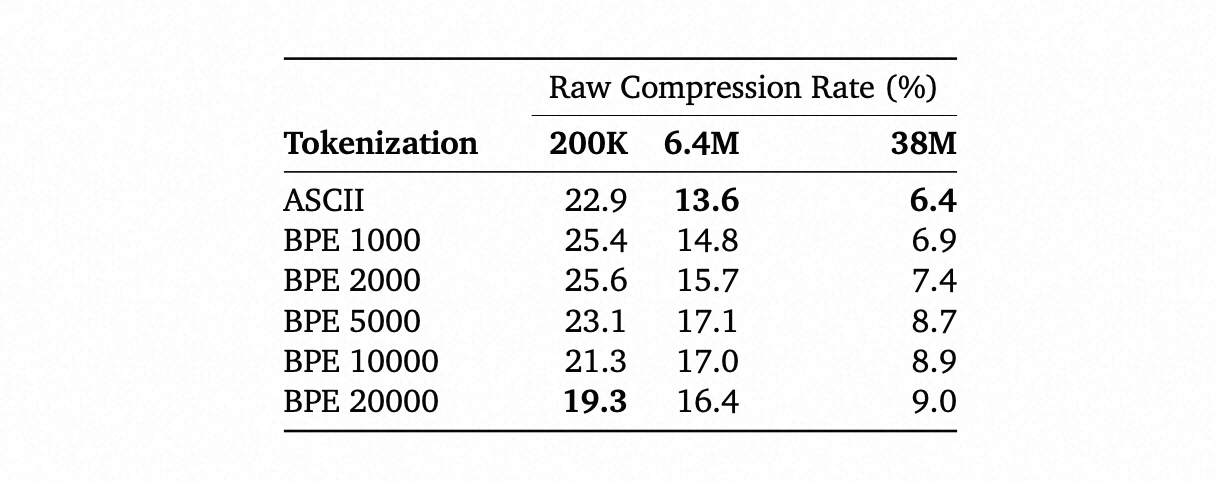
5. 疑问,思考和总结
看论文是有一个直观的疑问:使用大模型时,对同一个问题,输出的结果每次都是不一样的,怎么能保证解压缩时的结果的一致性呢?
其实大模型每次给出不同结果,是因为处理过程中故意增加了随机性,意图给出更丰富多样的回答。如果去掉随机性,得到的结果是完全一样的,比如哪个token的输出概率最大都是确定的。
还有这篇文章对于语言模型进行压缩的细节描述的太少了,甚至连一个示例图片或者示例伪代码都没有,导致读论文时很难想象这部分的细节,比如几个疑问,在文本上训练的语言模型是怎么在图像和语音任务上使用的,实际中怎么将语言模型当作算术编码来使用,等等。不知道作者为什么这么处理。
我觉得这篇论文可能会给相关研究方向带来新的想象空间,比如,文本语料上训练的模型也能在图像和音频数据上获得很好的压缩率,那是不是对于不同模态的输入,也可以设计同一个LLM来统一不同的任务呢?
再比如,既然像gzip这种传统压缩算法也能作为一个生成模型,而且运行成本远小于现有的LLM,那能否基于这种算法进行AI模型的演进呢?也许是一个更实用的方向。
总之这篇论文从压缩算法的角度提出了很多有意思有启发的观点,希望能对AI的研究产生新的前进推力。